编译原理实验2
¶实验内容:
输入一组正则表达式,输出其转换后的最简的确定有限自动机,并根据生成的确定有限自动机完成实验一的任务。(即完成词法分析任务)
输入一转换图,生成与之等价的正则表达式(未完成)
¶实验准备:
正则表达式的语义定义:符号表Σ上的正则表达式α定义一个Σ上的一个符号串的集合,记为L(α),其定义如下:
R::=R1R2 {L®=L(R1)∪L(R2)}
R::=R1R2 {L®=L(R1)L(R2)}
R::=R1* {L®=
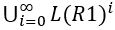
}
R::=(R1) {L®=L(R1) }
R::=a {a∈Σ,且 L®={a} }
R::=ε {ε不是Σ中的元素,L®={} }
转换图的定义:符号表Σ上转移T是一个带有权值的有向图T=(V,A),这是V是有向图T的顶点集合,其中的元素称之为状态,因此V亦称状态集,A是弧的集合,弧带有一个权α,其是Σ上的一个正则表达式。其满足如下条件:
- 存在唯一一个状态S0称为开始状态,其无引入弧
- 存在唯一一个状态S1称为终止状态,其无引出弧
转换图定义的语言记为L(T),其是Σ上的一个符号串的集合,Σ上的符号串α∈L(T)当且仅当存在一个由开始状态S0到终止状态S1的路径V0α1V1α2……Vn-1αnVn。
其中V0=S0,Vn=S1,(Vi-1,Vi, αi) (i=1,2,……,n)是T上的弧,且α∈L(α1)……L(αn)。
如果A中每个弧上的正则表达式是Σ上的一个符号或ε(无任何符号),则转换图称之为不确定的有限自动机。
如果A中每个弧上的正则表达式只能是Σ上的符号且任两个弧(V1,V2,α1)、(V’1,V’2,α’1),如果V1=V’1,则V2<>V’2。
¶基本算法:
将正则表达式转换成不确定的有限自动机:
对于一个正则表达式α,构造一个转移图,由开始状态S0引出一个到终止状态S1的弧,(S0,S1, α)。
如果有多个正则表达式α1,……,αn,先为每个αi(1<=i<=n)构造一个转换图Ti。建立一个新的转换图T,构造如下:添加一个Sb状态,为T的开始状态,对每个αi对应的转换图Ti的开始状态Si,添加弧(Sb,Si,ε)。添加一个新状态Se,为T的终止状态,对每个αi对应转换图Ti的终止状态S’i,添加弧(S’i,Sb,ε)。
重复如下操作,直到无状态转换图T无变化
对T中的每个弧(S1,S2,α),将α分解成两个正则表达式α1与α2由运算OP组成,即α=α1 OP α2。根据OP做如下操作:
OP是链接运算且α1与α2皆非ε(即不为空串),则于T中删除弧(S1,S2,α),于T中添加一个状态S,并将弧(S1,S,α1)与(S,S2,α2)添加到T中;
OP是链接运算且α1=(α’),α2=ε,则于T中删除弧(S1,S2,α),添加弧(S1,S2,α’)到T中;
OP是或运算,则于T中删除弧(S1,S2,α),将弧(S1,S2,α1)与弧(S1,S2,α)添加到T中;
OP是闭包运算,且α2=ε,则于T中删除弧(S1,S2,α),于T中添加一个新状态S,并将弧(S1,S,ε)、(S,S,α1)及(S,S2,ε)添加到T中。
将不确定有限自动机确定化:不确定有限自动机记为NFA,则按照如下操作构造一个确定有限自动机DFA其与NFA等价。
构造NFA中的状态集组成的集合F,初始时F为空;
将NFA状态集closure({S0})添加到F中(S0是NFA的开始状态);
重复如下操作,直到F中无新元素增加止
对F中任一元素S(NFA的状态集),对符号表Σ中的每个符号a,将closure(Sa)添加到F中。有关Sa定义如下:
Sa={s 于S中存在一个状态s’,使得(s’, s, a)是NFA中的一个弧}
定义转移图T如下:则以F中元素为状态,对F中每个元素S,则有弧(S,Sa, a)。如果F中的元素S(NFA的状态集)中含有NFA的终止状态,则其S是T的终止状态。T的开始状态是closure({S0})。
确定有限自动机的化简操作:
将DFA化简为最简单的sDFA操作如下:
建立DFA状态集的一个分划:π,初始时π中仅有两个集合,一个是由DFA中状态组成的集合,另一个不是终止状态组成的集合。
重复如下操作
对符号表Σ上的每一个符号a做如下操作
建立一个空分划π0(即π0是一个空的状态集合之集合)
对π中的每个集合S0
对π中的第i个集合Si
令S0,i,a={s∈S0 存在弧(s,s1,a),这里s1∈Si}
If(S0,i,a非空)将S0,i,a添加到π0中
将π0记之为π
¶自动生成词法分析程序:
类Disjoint:并查集, 用于计算等价关系;
类Automata:有穷自动机:
- 有穷状态集(对应有向图中的节点)
- 输入字母表(状态转移边的标注)
- 状态转移规则(对应有向图中的边)
- 初始状态
- 终止状态集
检查转移图的合法性:
- 起始状态必须在状态集中
- 终止状态必须在状态集中
检验是否为确定的有穷自动机(DFA) 标准:
- 不能有 epsilon 作为输入的字母
- 存在某状态对于某字母有多种后继状态
¶实验过程:
- 编写代码
源码:Randall Chu / 编译原理实验2 · GitLab (zhuanjie.ltd)
- 测试运行(实验环境Windows11 Python3.10 pycharm),如图:
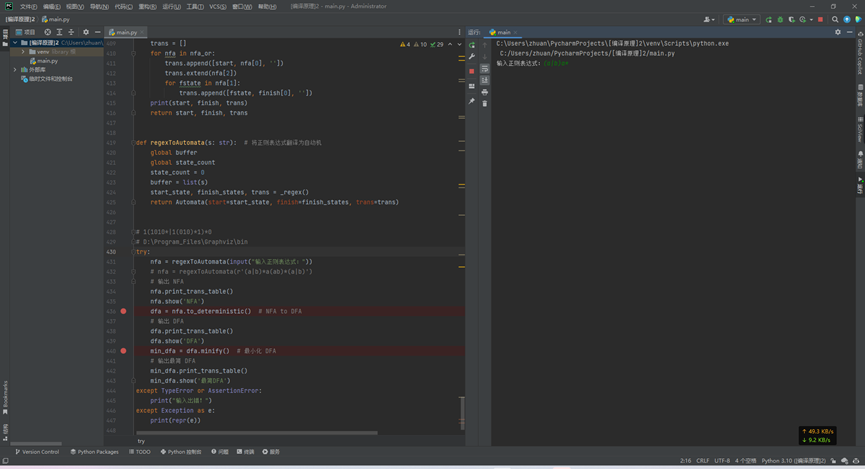
- 输出信息:
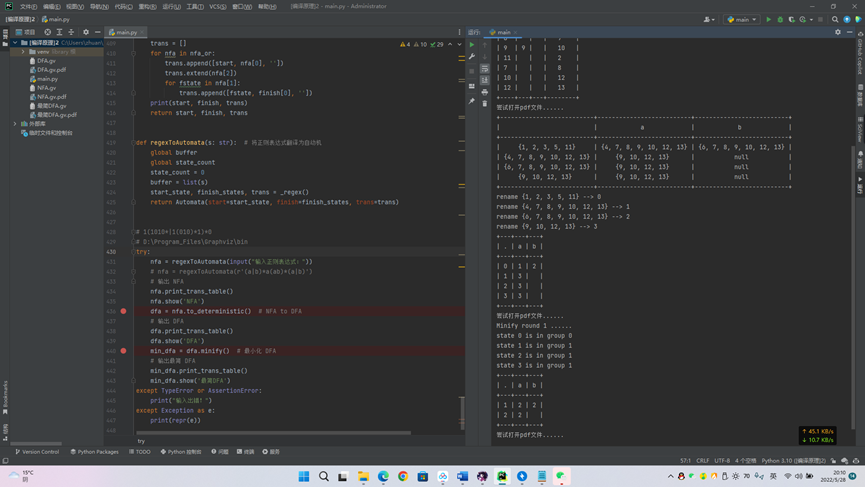

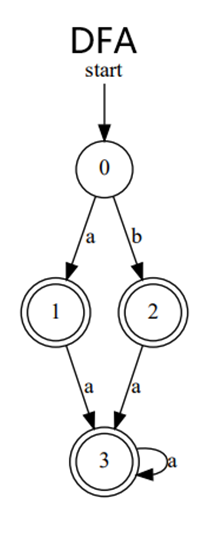
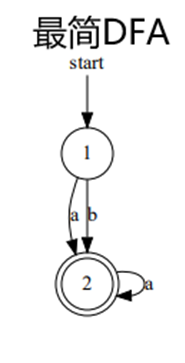
实验总结:
通过本次实验我学会了从正则表达式转NFA(不确定的有穷自动机)、NFA转DFA(确定的有穷自动机)和DFA的最小化。同时我也尝试输出了自动机的转移矩阵和输出自动机的状态转移图。输出自动机的状态转移图使用的是图形可视化软件Graphviz的使用,他能够将将结构信息表示为抽象图形和网络图。在编程过程中程序抛出了ExecutableNotFound的异常信息,经过检查发现为未将Graphviz的安装地址置于系统的环境变量中。状态图中:以圆圈表示状态(圆圈内为状态名),箭头表示状态转移边。以start标记引出箭头指向起始状态,以双圈表示终止状态。