编译原理实验3

语义分析常用算法的实现及应用实验
以某种方式输入一个上下文无关文法，构造其LL分析表、算符优先分析表及LR分析表，并能够差别一个字符串是否是给定文法中的句子

¶实验内容

以某种方式输入一个上下文无关文法，构造其LL分析表、算符优先分析表及LR分析表，并能够差别一个字符串是否是给定文法中的句子

在实验一或实验二的基础上，建立一个表达式的文法，并生成该表达式的计算程序。

¶实验目的

1、进一步理解文法特别是上下文无关文法相关概念

2、掌握求First集、Follow集、FirstVt集及LastVt集算法，并能够应用其构造文法的LL分析表、算符优先分析表及LR分析表

3、通过分析LL(1)文法、算符优先文法及LR(1)文法进一步理解自动编程方法

¶实验准备

¶文法的输入

在一个文框中输入文法规则，每个规则占一行，文法规则以如下形式输入：左部符号::=文法规则右部符号串

第一条规则的左部符号即为文法的开始符号。一个（左部符号或右部符号）符号使用一个字符串表示，如果有两个形如“A::=α和A::=β”的规则，则可以合并成“A::=α｜β”。

¶左部符号与右部符号的确定

左部符号的确定：位于每个规则左部即为左部符号。

右部符号的确定：将每个右部符号串使用左部符号之符号串将其分隔成字符串序列，则不是左部符号之符号串即为右部符号或右部符号串组成的字符串。分隔的原则是“长度优先”，即一个长左部符号串不得再分隔成字符串序列，一个字符串优先使用较长的左部符号之符号串分隔。

¶文法的存储表示

关键记数：左部符号个数nVn，右部符号个数nVt，规则个数nRule

符号表：使用一个字符串数组存储左部及右部符号，左部符号字符串在前，右部字符串在后。每个符号使用其在符号表中的下标表示，当下标是nVn+nVt时，符号是空符号（ε），当下标是nVn+nVt+1时，符号是结束符号（#）。

规则列表：使用一个规则数组存储规则列表，一条规则由左部符号（使用其在符号表中下标表示）及左部符号序列（即符号之下标序列）表示。

¶基本操作算法描述

¶求First集算法

先初始化非终结符的First集为空，初始化终结符的First集合为自己；开始循环，当First集没有更新就结束循环。循环内：新建一个标记flag初始化为False，遍历所有非终结符，每次遍历非终结符时遍历所有产生式。新建一个标记mark初始化为True，当mark为True并且遍历到产生式的末尾就结束。如果还存在没有添加的即First[Yi]中没有ε，则将First[Yi]添加到First[X]中，同时将标记mark更新为False。如果是第一个符号，则将First[Yi]中的非ε添加到First[X]中，同时flag标记更新为True。如果Yi不能推出ε就标记为False；如果所有的Yi都推出ε则将ε添加到First[X]中。

def getFirst() -> None:
    global non_term, term, First
    # 初始化非终结符的First集为空
    for it in non_term: First[it] = set()
    # 初始化终结符的First集合为自己
    for it in term:
        First[it] = set(it)
    flag = True
    while flag:  # 当First集没有更新就结束
        flag = False  # 新建一个标记flag初始化为False
        for X in non_term:  # 遍历所有非终结符
            for Y in production[X]:  # 遍历所有产生式
                i = 0
                mark = True  # 新建一个标记mark初始化为True
                while mark and i < len(Y):  # 当mark为True并且遍历到产生式的末尾就结束
                    if not First[Y[i]] - set(epsilon) <= First[X]:  # 还存在没有添加的
                        # print('First[' , X, '] = ', "   ", First[X], 'First[', Y[i] , '] = ' , First[Y[i]])
                        # First[Yi] 中没有 ε
                        if epsilon not in First[Y[i]] and Y[i] in non_term and i > 0:  # 如果不是第一个符号
                            First[X] = First[Y[i]]  # 将 First[Yi] 添加到 First[X] 中
                            mark = False  # 标记更新为False
                        else:  # 如果是第一个符号
                            First[X] = First[Y[i]] - set(epsilon)  # 将 First[Yi] 中的非 ε 添加到 First[X] 中
                            flag = True  # flag标记更新为True
                    if epsilon not in First[Y[i]]:  # 如果 Yi 不能推出 ε 就标记为 False
                        mark = False  # mark标记更新为False
                    i += 1
                if mark:  # 如果所有的 Yi 都推出 ε
                    First[X] = set(epsilon)  # 将 ε 添加到 First[X] 中
return None

¶求Follow集算法

初始化后将 # 号加入到Follow[s] 中，新建一个标记flag初始化为True。开始循环，当Follow集不再更新，算法结束。循环内：标记flag初为False，遍历所有非终结符。每次遍历非终结符时遍历所有产生式，扫描产生式时遍历所有产生式的每一个符号。bi 是终结符则跳过，否则新建一个标记mark初始化为True，遍历所有产生式的每一个符号。如果可以更新则将 First[Bj] 中的非 ε 添加到 Follow[Bi] 中，设置标记flag为True。如果 Bj 不能推出 ε 就标记为 False，设置mark标记为False。判断mark，如果为True，那么A->αBβ and β->ε。如果可以更新，将 Follow[A] 添加到 Follow[B] 中，设置flag为True。

def getFollow() -> None:
    global non_term, term, First, Follow, start_sym
    for A in non_term:
        Follow[A] = set()  # 初始化
    Follow[start_sym].add(end_sym)  # 将 # 号加入到Follow[s] 中
    flag = True  # 新建一个标记flag初始化为True
    while flag:  # 当Follow集不再更新，算法结束
        flag = False  # 标记flag初为False
        for A in non_term:  # 遍历所有非终结符
            for B in production[A]:  # 遍历所有产生式
                for i in range(len(B)):  # 遍历所有产生式的每一个符号
                    # bi 是终结符则跳过
                    if B[i] in term:
                        continue
                    mark = True  # 新建一个标记mark初始化为True
                    for j in range(i + 1, len(B)):  # 遍历所有产生式的每一个符号
                        if not First[B[j]] - set(epsilon) <= Follow[B[i]]:  # 可以更新
                            Follow[B[i]] = First[B[j]] - set(epsilon)  # 将 First[Bj] 中的非 ε 添加到 Follow[Bi] 中
                            flag = True  # 发生了改变
                        if epsilon not in First[B[j]]:  # 如果 Bj 不能推出 ε 就标记为 False
                            mark = False  # 设置mark标记为False
                        break
                    if mark:  # A->αBβ and β->ε
                        if not Follow[A] <= Follow[B[i]]:  # 可以更新
                            Follow[B[i]] = Follow[A]  # 将 Follow[A] 添加到 Follow[B] 中
                            flag = True  # 发生了改变
    return None

¶实验过程

1. 编写代码

Randall Chu / 编译原理实验3 · GitLab (zhuanjie.ltd)

2. 测试文法

LL1文法

E->TA
A->+TAε
T->FB
B->*FBε
F->i(E)

非LL1文法

S->AB
S->bC
A->ε
A->b
B->ε
B->aD
C->AD
C->b
D->aS
D->c

3. 测试运行(实验环境Windows11 Python3.10 pycharm)，如图：

4. 输出信息

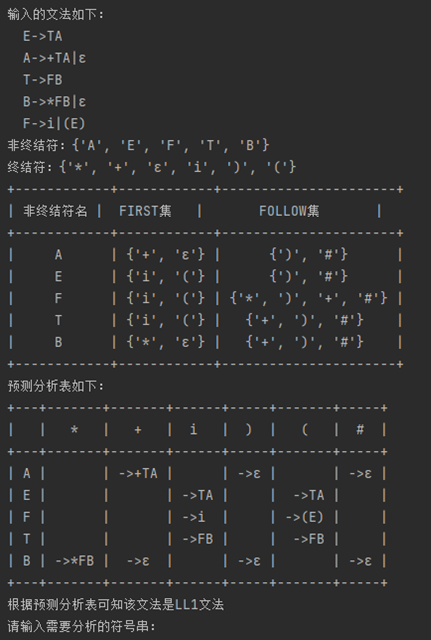
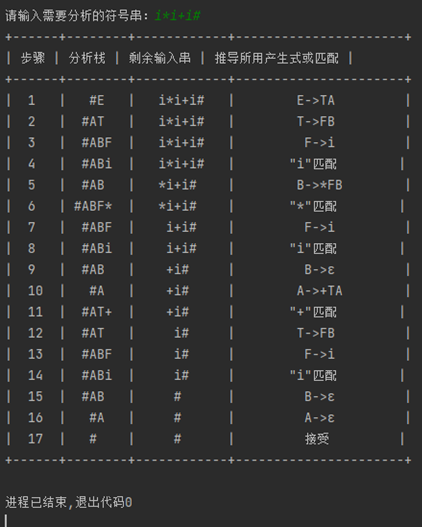
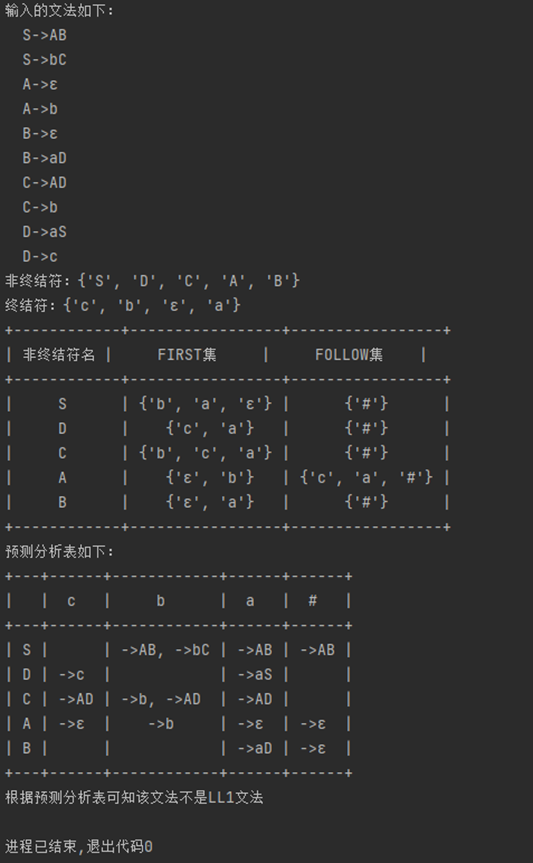
¶实验总结

通过本次实验我进一步理解了文法特别是上下文无关文法相关概念，掌握了求First集、Follow集、FirstVt集及LastVt集算法，并能够应用其构造文法的LL分析表、算符优先分析表及LR分析表。我也通过分析LL(1)文法、算符优先文法及LR(1)文法进一步理解了自动编程方法。刚刚写完分析符号串逻辑思路代码，这个心情是无比激动的，但是又有诸多的bug，内心是无比崩溃的，然后经过一行一行的修改，慢慢的调终于弄好了。