浅读算法导论——3.1渐近记号

渐近记号适用于函数，Θ(n2)就是函数an2+bn+c。渐近记号适用于刻画算法运行时间、算法使用的空间数量等的函数

O(1)<O(log2(n))<O(n)<O(nlog2(n))<O(n2)<O(2n)<O(n!)<O(nn)

¶Θ记号、O记号、Ω记号

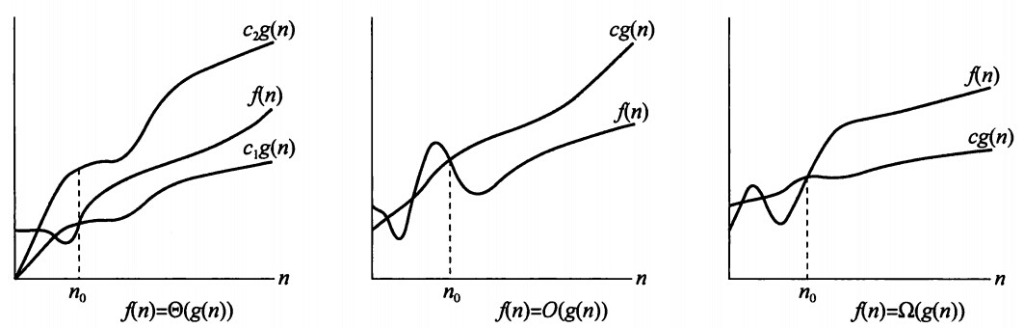
¶Θ记号

Θ记号限制一个函数在常量因子内，对所有n≥n0时，函数f(n)在一个常量因子内等于g(n)，我们称g(n)是f(n)的一个渐近紧确界

¶定义

对一个给定的函数g(n)，用Θ(g(n))表示以下函数集合

Θ(g(n)) = {f(n) 存在正常量c1，c2和n0，使得对于所有的n≥n0，有0≤c1g(n)≤f(n)≤c2g(n)}

若存在正常量c1和c2，使得对于足够大的n，函数f(n)能夹入c1g(n)和c2g(n)之间，则f(n)属于集合Θ(g(n))。所以可以记f(n)∈Θ(g(n))，通常记为f(n)=Θ(g(n))

我们称g(n)是f(n)的一个渐进紧确界

Θ(g(n))的定义要求每个成员f(n)∈Θ(g(n))均渐近非负，即当n足够大时，f(n)非负，否则集合Θ(g(n))为空

¶非形式化概念

对于Θ记号的非形式化概念：扔掉低阶项，并忽略最高项前的系数

原因：当n足够大时，即使最高项的一个很小的部分都足够支配所有的低级项

e.g.证明(1/2)n2-3n=Θ(n2)
解：根据Θ记号定义，假设存在c1，c2和n0使得对所有的n≥n0，有：
    0 ≤ c1n2 ≤ (1/2)n2-3n ≤ c2n2
    两边同时除以n2得：
    c1 ≤ (1/2)-(3/n) ≤ c2
    对于c1=1/14， c2=1/2， n0=7时，不等式恒成立，原式得证。

对于任意二次函数f(n)=an2+bn+c，其中a、b和c均为常量且a>0。根据非形式化概念可得f(n)=Θ(n2)，证明时取c1=a/4， c2=7a/4， n0=2*max{ b/a, √(c/a) }，可证明对于所有的n≥n0，有0≤c1n2≤an2+bn+c≤c2n2

¶O记号

O记号为函数给出一个在常量因子内的上界

¶定义

Θ记号渐进地给出一个函数的上界和下界，当只有一个渐进上界时，用O记号表示

O(g(n)) = {f(n) 存在正常量c和n0，使得对于所有的n≥n0，有0≤f(n)≤cg(n)}

对在n0及其右边的所有值n，函数f(n)的值总小于或等于cg(n)

f(n)=Θ(g(n))里面蕴含着f(n)=O(g(n))，在集合中有Θ(g(n))⊆O(g(n))

对于任意二次函数an2+bn+c，其中a>0，在Θ(n2)中的证明也证明了在O(n2)中

ESP.当a>0时，对于任意线性函数an+b也在O(n2)中，证明取c=a+b，n0=max{ 1, -b/a }，有(a+b)n2 ≥ an+b ≥ 0

我们仅仅要求g(n)的某个常量倍数是f(n)的渐进上界，而不是要求他是一个多么紧确的上界

O记号是描述上界的，当它用来限制算法的最坏情况运行时间，我们说运行时间为O(n2)时，指的是存在一个O(n2)的函数f(n)，使得对于n的任意值，不管选择什么特定的规模为n的输入，运行时间上界都是f(n)，也就是说最坏情况运行时间是O(n2)

¶Ω记号

Ω记号为函数给出一个在常量因子内的下界

¶定义

Ω记号提供了渐进下界

Ω(g(n)) = {f(n) 存在正常量c和n0，使得对于所有的n≥n0，有0≤cg(n)≤f(n)}

对在n0及其右边的所有值n，函数f(n)的值总大于或等于cg(n)

对于任意两个函数f(n)和g(n)，有：f(n)=Θ(g(n))⇔f(n)=O(g(n))且f(n)=Ω(g(n))

¶等式中的渐进记号

当渐进记号独立于等式（或不等式）的右边时，表示集合成员关系

e.g.n=O(n2)表示n∈O(n2)

当渐进记号出现于某个公式里时，它表示某个我们不关注名称的匿名函数

e.g.公式2n2+3n+1=2n2+Θ(n)表示2n2+3n+1=2n2+f(n)，其中f(n)为我们不需要关注的匿名函数

渐进记号出现在等式左边表示无论怎样选择等号左边的匿名函数，总有一种办法来选择等号右边的匿名函数使得等号成立。对于任意函数f(n)∈Θ(n)，存在某个函数g(n)∈Θ(n2)，使得对于所有的n有2n2+f(n)=g(n)，即等式右边比等式左边提供的细节更粗糙

e.g.2n2+3n+1 = 2n2+Θ(n) = Θ(n2)

¶o记号和ω记号

¶o记号

由O记号提供的渐进上界可能是也可能不是渐进紧确的。如界2n2=O(n2)是渐进紧确的，但是2n=O(n2)不是

¶定义

o记号表示非渐进紧确的上界

o(g(n)) = {f(n) 存在正常量c和n0，使得对于所有的n≥n0，有0≤f(n)≤cg(n)}

当n趋向于无穷时，函数f(n)相对于g(n)来说变得微不足道了

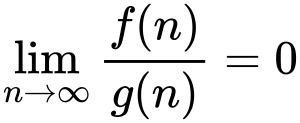
¶ω记号

¶定义

ω记号来表示非渐进紧确的下界，定义方式是：f(n)∈ω(g(n))当且仅当g(n)∈o(f(n))

ω(g(n)) = {f(n) 存在正常量c和n0，使得对于所有的n≥n0，有0≤cg(n)≤f(n)}

例如，n2/2=ω(n)，但是n2/2≠ω(n2)，关系f(n)=ω(g(n))蕴含着

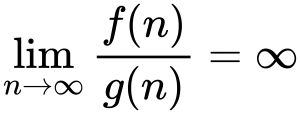
¶渐近记号Θ、Ο、Ω、o、ω之间的关系

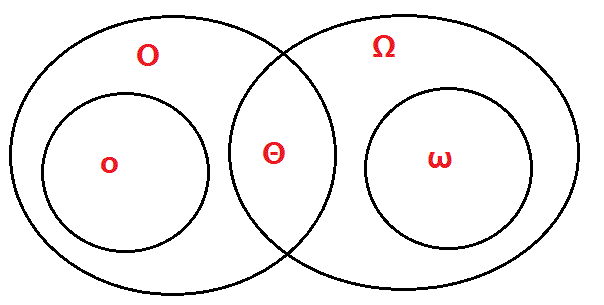
假定f(n)和g(n)渐进为正

¶传递性

f(n) = Θ(g(n)) 且 g(n) = Θ(h(n)) 则 f(n) = Θ(h(n))

f(n) = Ο(g(n)) 且 g(n) = Ο(h(n)) 则 f(n) = Ο(h(n))

f(n) = Ω(g(n)) 且 g(n) = Ω(h(n)) 则 f(n) = Ω(h(n))

f(n) = o(g(n)) 且 g(n) = o(h(n)) 则 f(n) = o(h(n))

f(n) = ω(g(n)) 且 g(n) = ω(h(n)) 则 f(n) = ω(h(n))

¶自反性

f(n) = Θ(f(n))

f(n) = Ο(f(n))

f(n) = Ω(f(n))

¶对称性

f(n) = Θ(g(n)) 当且仅当 g(n) = Θ(f(n))

¶转置对称性

f(n) = Ο(g(n)) 当且仅当 g(n) = Ω(f(n))

f(n) = o(g(n)) 当且仅当 g(n) = ω(f(n))

符号	含义	类比
Θ	渐进紧确界	相当于“=”
O	渐进上界	相当于“≤”
Ω	渐进下界	相当于”≥”
o	渐进非紧的上界	相当于”<”
ω	渐进非紧的下界	相当于”>”

若f(n) = o(g(n))则称f(n)渐进小于g(n)，若f(n) = ω(g(n))则称f(n)渐进大于g(n)

¶三分性

虽然所有实数都可以比较，但是不是所有函数都可以渐进比较的。两个函数f(n)和g(n)可能f(n) = Ο(g(n))和f(n) = Ω(g(n))都不成立

如：n和n1+sin(n)，因为1+sin(n)在0到2之间摆动